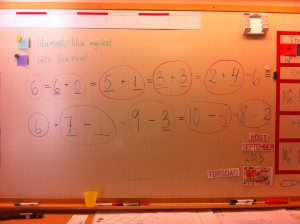En fantastisk dag – en hel dag med matematik för alla elever på vår F- 6 skola! Rena rama lyckan och vilket gensvar, vilket lärande, vilka grymma elever, wow-känsla under hela dagen. Vår skolas vision fanns levande under hela dagen hos alla såväl personal som elever:
 Under året har idén om en matematikdag grott och under matematikbiennalen kom underlaget för planering till. Främst var det Lina Boman, som har funderat och då och då frågat oss i mattegruppen om vi inte skulle kunna ha en matematikdag. När Känguruproven skulle beställas i början av vårterminen kom idén att dessa skulle vi kunna använda – men hur? Tidsaspekten gjorde att vi insåg att årets tester skulle vi inte kunna använda tyvärr.
Under året har idén om en matematikdag grott och under matematikbiennalen kom underlaget för planering till. Främst var det Lina Boman, som har funderat och då och då frågat oss i mattegruppen om vi inte skulle kunna ha en matematikdag. När Känguruproven skulle beställas i början av vårterminen kom idén att dessa skulle vi kunna använda – men hur? Tidsaspekten gjorde att vi insåg att årets tester skulle vi inte kunna använda tyvärr.
Vi var tre lärare som åkte till årets matematik biennal – Sameh Ekström, Lina Boman och jag, vi fick massor av goda idéer med oss. Under sista dagen snickrade Lina och Sameh ihop en stomme till vår kängurudag med idéer från olika föreläsare som vi lyssnat på. En GOTD med fakta om Australien blandat med olika matteövningar på olika nivåer. I starten hade vi en tanke på att göra ett digitalt escape room men det blev ett minst lika bra analogt escape room. I fantasin flög hela skolan iväg på en rundresa i hela Australien. Fakta om olika platser blandades med matematikuppgifter under en hel skoldag. Marcus Jacobsson gjorde ett schema för dagen, ca 580 elever skulle slussas runt på olika stationer, till slut så fanns det 6 stationer – i varje klassrum 3 uppdrag, lunchen och 2 utestationer – ett pussel som funkade utmärkt. Lunch serverades ute av köket, som också ställde upp lite extra den här dagen och serverade supergoda grillade hamburgare till både vår f-6 skola och vår grannskola med ca 500 elever i åk 7-9.
Vi använde oss av spel, ekvationer, sudoku, sant eller falskt övning och geometriproblem. Alla uppgifter fanns på olika nivåer för att alla skulle kunna vara med.
- Spelet fick vi från en föreläsning av Maria Lindroth och Per Berggren på matematikbiennalen.
- Sudoku – Tyvärr kan vi inte dela med oss av sudokun för de har vi tagit från vårt läromedel Favorit matematik. Det finns bra sudokun på olika nivåer i läromedlet vilket gjorde att vi med lite pyssel kunde se till att få samma kod oavsett nivå på sudoku.
- De geometriska problemen har vi hittat på olika ställen, bla i NCMs strävor och hos Ulrica Elisson, Ullis skolsida.
- Ekvationerna är egen tillverkning.
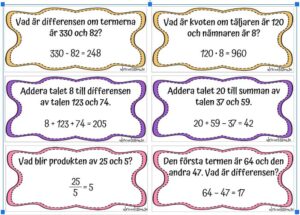
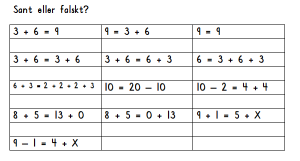
- Sant eller falskt uppgifterna är från mina tidigare kort och från Ullis skolsida.
Här hittar ni
- presentationen:
https://docs.google.com/presentation/d/1cIuNOMBVBdK7AQ8VfHE4CjRoMedigVxrBbI1fPclDVg/copy
- Delbart Allt material – Grupphäfte alla
- Delbart Lärarhäfte

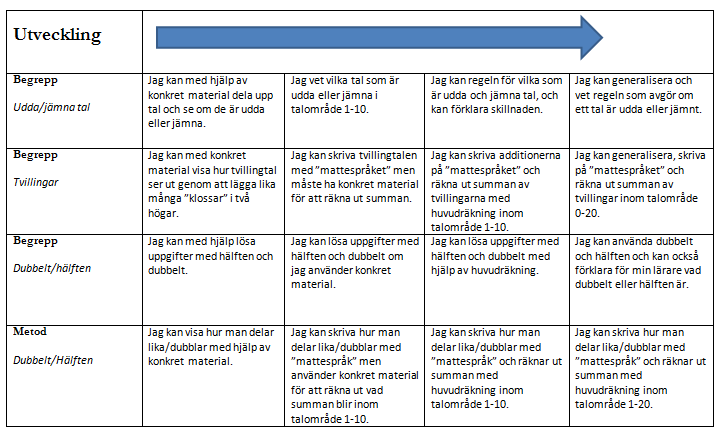
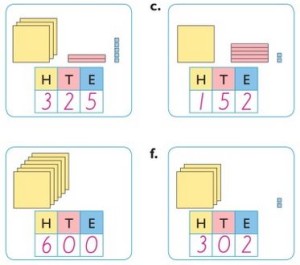
Ekvationer f – 1
Ekvationer f – 3
Ekvationer 4 – 6
















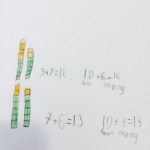










![IMG_4455[1]](http://mattefroken.se/wp-content/uploads/2014/09/IMG_44551-e1411502189812-224x300.jpg)