När man går leende in i klassrummet och ännu mer leende när man går ut efter en timmes matematiklektion mår man så himla bra. Idag var det lektion från matematiklyftet om likhetstecknet som fanns på programmet. Vi startade med en liten uppvärmning med några algebra uttryck:
9 + 3 = X + 4 9 + 3 = 8 + 4 9 + 3 = 12 + 4 9 + 3 = 16 + 4
Uppgiften var en repetition från förra veckans lektion så eleverna var insatta i problematiken. Vi tänkte återigen högt tillsammans på hur eleven som löst uppgifterna hade tänkt och hur man skulle kunna förklara för någon annan om hur man gör.
Eleverna är så underbart tydliga och klara på hur man gör när vi diskuterar, de förklarar begrepp och tankar genom att använda matematiska termer.
Lektionen fortsatte lite utanför planen för jag ville se hur långt vi kunde komma eftersom starten gick så bra. Jag fortsatte på det andra talet och utökade på ena sidan likhetstecknet 4 + 9 + 3 = 8 + 4 och undrade vad vi nu skulle göra. Det gick en liten suck genom klassrummet, en härlig suck av förståelse och mot en knäpp fråga(lärare). Flera utbrast rakt ut att man måste göra samma ska på båda sidor om likhetstecknet. Fortsatte att vara lite tramsig och förstod ingenting, de fick vara väldigt tydliga i sin förklaring om vad och varför jag skulle göra som de ville. Nu hade eleverna fått som de ville och det stod
4 + 9 + 3 = 8 + 4 + 4, de var rätt nöjda! Då ställer jag till det igen:
4 + 9 + 3 = 8 + 4 + 4 + 287
Jag är rätt nöjd blev ju snyggt, gick därifrån för att sätta igång resten av arbetet. Det är fullt fokus på tavlan! Eleverna diskuterar lite lågt med varandra, inte alla – en elev sitter med ett leende på läpparna med armen i luften. Någon säger att så stora tal brukar vi inte ha, någon annan tycker att jag ska hämta miniräknare och den leende eleven sitter kvar med armen i luften. Plötsligt säger en röst bara:
– Aha!
Då är det som om en vind går fram genom klassrummet och fler och fler leenden och händer i luften. Jag är lite upptagen och de får aktivt påvisa att de inte är nöjda med min insats på tavlan. jag ger ordet till den första leende eleven som borde vara trött i armen nu;
– Du måste göra samma sak på andra sidan, säger eleven glatt, och förklara tydligt att det ska stå
287 + 4 + 9 + 3 = 8 + 4 + 4 + 287
Någon yttrar att det var taskigt att ta så stort tal, då kan jag inte låta bli att köra en runda till…skriver:
7851 + 287 + 4 + 9 + 3 = 8 + 4 + 4 + 287
och undrar hur de nu ska göra. Längst fram sitter en lite elev och pustar lite tyst:
– Kan du ta och skriva de där 4 siffrorna på andra sidan nu på direkten!
Kompisen vid sidan om förtydligar:
– Nu får du skriva sjutusenåttahundrafemtioett på andra sidan också menar hen.
7851 + 287 + 4 + 9 + 3 = 8 + 4 + 4 + 287 + 7851
I mitt öra klingar dock den där viskningen så mycket högre, eleven har faktiskt precis bevisat att hen kan påvisa likhetstecknets betydelse och skulle kunna göra samma sak själv om hen hade tal att laborera med. Glädje i ett klassrum!
Nu satte vi igång med arbetet i grupper:
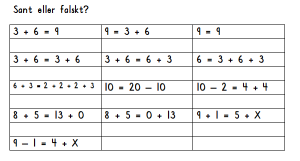 Grupperna är väl inarbetade och eleverna satte igång med fullt fokus och energi på uppgifterna. Deras uppgift var att hitta intressanta uppgifter som vi var tvungna att hjälpa till med. Rätt kvickt fick de klart för sig att det bara var en uppgift som behövde ändras. Här gick det verkligen så fort att de tydligt påvisade att de inte räknat ut hela uppgifterna utan de hade verkligen jämfört talen på de båda sidorna om likhetstecknet. Vi skrev upp talet som de ville rätta till och lade sedan vår energi på att hitta flera olika lösningar tillsammans. Så många lösningar med härliga kommentarer! 60 minuter ljuvlig kreativ kommunikativ undervisning!
Grupperna är väl inarbetade och eleverna satte igång med fullt fokus och energi på uppgifterna. Deras uppgift var att hitta intressanta uppgifter som vi var tvungna att hjälpa till med. Rätt kvickt fick de klart för sig att det bara var en uppgift som behövde ändras. Här gick det verkligen så fort att de tydligt påvisade att de inte räknat ut hela uppgifterna utan de hade verkligen jämfört talen på de båda sidorna om likhetstecknet. Vi skrev upp talet som de ville rätta till och lade sedan vår energi på att hitta flera olika lösningar tillsammans. Så många lösningar med härliga kommentarer! 60 minuter ljuvlig kreativ kommunikativ undervisning!



