Etikettarkiv: matematik

En inspirerande matematikbiennal i backspegeln

Publicerat av
Svara

Fullt med matematikinspiratörer, matematiklärare och forskare möttes under 2 dagar i Karlstad på en matematikbiennal. För min del var det sjunde gången jag hade möjligheten att få lyssna på föreläsare och samtala med andra kollegor från olika områden och delar av vårt avlånga land. Jag åkte iväg med höga förväntningar som verkligen infriades denna gången, det var hög nivå på årets biennal, ett urval som verkligen gjorts med omsorg.

För min del valde jag att lyssna på följande olika inspiratörer:

MAM – mestre Ambisiös matematikundervisning, Laering for laerer og elever
med Svein H Torkildsen, Trondheim

Upptäck Singapore Math och hur modellen används i svenska klassrum
med Pia Agardh och  Josefine Rejler

Textuppgifter med Singapore-metoden för åk 1-5
med Doris Lindberg, Stockholm

Matematisera mera – att styra och stötta det matematiska samtalet
med Cecilia Kilhamn, Göteborg

Nyanländas lärande i matematik
med Saman Abdoka, Eskilstuna

STL, digitala verktyg som hävstång för lärande i matematik
med Anna Pilebro Bryngelsson, Frida Lindell, Sollentuna

Det aktiva matematikklassrummet
med Åsa Brorsson, Mölndal

Att undervisa i matematik med digitala verktyg
med Ulrika Ryan, Malmö

En undervisningsmodell för taluppfattning i lågstadiet
med Ola Helenius, Göteborg, Anna Ida Säfström; Halmstad, Görel Sterner, Göteborg

Så många olika föreläsningar och ändå fanns det en röd tråd genom alla. En lyckad undervisning handlar om struktur och om att vara förberedd. Att tänka cykliskt  runt undervisningen och ge eleverna en igenkänning stärker lärandet. Här kommer mina tankar efter dagarna i Karlstad.

Läraren styr i klassrummet, ser till att samtalet flyter och att eleverna lär sig kommunicera i matematik, lärandet i matematik sker genom kommunikation. Läraren genomför – ORKESTRERING, ett nytt ord/begrepp som sätter fingret på lärarrollen i klassrummet. Flera av föreläsarna poängterade just detta, vikten av att styra och leda undervisningen och dialogen i klassrummet. Att använda olika sätt så att alla elever får möjlighet att samtala, ha en lärkompis som eleven känner sig trygg med, parvis och sedan återkoppla tillsammans för att se det gemensamma lärandet.

I boken ”Tänka, resonera och räkna finns en cirkulär arbetsgång som i stort sätt är hållbar oavsett med vilken ålder du arbetar. På bilden har jag förändrat strukturen i undervisningens upplägg för att passa in i den i mitt tänk. Jag tycker att det är bra att ha en tanke som jag vet hjälper mig att följa eleverna och att få in alla olika delar i undervisningen. Det är inte alltid som upplägget påbörjas och avslutas under en lektion men en sekvens/del får ofta en cirkulär gång.

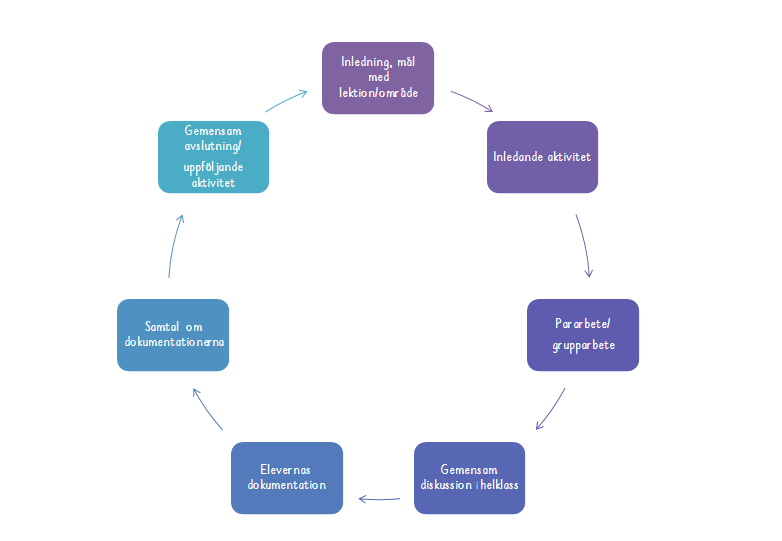
Givetvis finns det vissa moment som kan vara ren träning men de behöver ändå en start tillsammans för att få med alla elever och öppna upp tankarna mot matematiken. Att under träning då och då knyta ihop och fundera högt tillsammans ger eleverna stöttning och de kan hitta strategier som stärker dem.

Singaporemetoden arbetar mycket med struktur och genom problemlösning får eleverna lösa problem tillsammans och diskutera aktivt. Man visar lösningar, diskuterar hållbarhet, testar varandras strategier och modellerar. Ca 2/3 av undervisningen sker tillsammans. I stort sett så stämmer ovanstående även här. Man delar in undervisningen i huvudräkning, problemlösning och taluppfattning.

Att ha små små hjälpmedel under lektioner för att inte störa är värdefullt. Tex istället för handuppräckning när du förstår kan man ha färgkoder som trafikljus el liknande, men jag gillade ”tumme upp” som Cecilia Kilhamn visade i några filmer. Så enkelt helt tyst och knappt synligt för omgivningen. Cecilia visade också på vitsen med att läraren skulle dirigera i klassrummet. Dirigenten flyter runt och lyssnar in under lektionen för att sedan kunna knyta samman. Ge eleverna små återkopplingar genom att ta upp deras tankar i sitt eget resonemang. Viktigt att ta med dem i samtalet.

Saman Abdoka tog oss in på en snabb rundvandring i de nyanländas matematik. Små tips för att ge förståelse för varför elever kanske räknar ut tal på ett visst sätt eller varför de skriver tid på ett helt annat sätt än vad vi gör. Att komma till Sverige och förstå att man kan skriva 2,5 kg men inte 2,5 kr, det är ju precis samma sak egentligen för en nolla i slutet påverkar ju inte i detta fallet talet.En insyn att det finns en uppsjö av olikheter på skolgång hos eleverna. Hur vi tex säger talen mellan 11 – 99, vilken struktur språken har. Jag hade gärna lyssnat ännu längre på Saman Abdoka för att kunna ta till mig allt han kunde dela med sig av. Ett stöd för att hjälpa oss förstå våra nyanlända elever. Hur många lärare sorterar bort de ord i textuppgifter som inte är matematiska och som inte behövs för att lösa uppgiften?

STL- skriva sig till lärande i matematik, är ett sätt att dokumentera elevernas kunnande och de utmanas när de måste sätta ord på sitt lärande. Det här kommer jag att ta till mig och utnyttja i vissa moment. Även här var det strukturen i undervisningen som gav kunskapsutveckling. Det kommer att bli flera samtal med Frida Lindell om detta!

Att avsluta föreläsningarna med en fortsättning på boken ”Tänka, resonera och räkna i förskoleklassen” av Ola Helenius och Anna Ida Säfström med Görel Sterner som sufflerade vid behov var en höjdpunkt. Deras tankar tar jag med mig direkt och tänker utnyttja redan under våren i åk 1.

Sammanfattningen av Matematikbiennalen i Karlstad 2018 är verkligen bra! En överraskande hög nivå och även om inte allt var nytt och flera saker som man nickade åt så är det just igenkänningen av de viktiga delarna i undervisningen som jag tar med mig! Samtala med eleverna följ en struktur och återkoppla med strategier som eleverna behöver för sitt lärande, låt dem undersöka men knyt ihop delarna tillsammans och låt eleverna även få sätta ord på sin kunskap.

(Kanske blir det så småningom fördjupande inlägg om några av delarna i detta inlägg.)

Mattekort

Publicerat av
Svara

Vi håller på att träna på lilla plus och minus. Till detta har vi gjort kort och varje vecka delar vi ut kombinationerna till ett nytt tal. Nu är vi framme vid talet 10.

Här hittar ni korten till talen 5-10 med både addition och subtraktion:

matematik kort talet 5

matematik kort talet 6

matematik kort talet 7

matematik kort talet 8

matematik kort talet 9

matematik kort talet 10

Samtidigt tränar eleverna varje dag på Vektor där de möter utmaningar på sina egna nivåer i sin egen takt.

 

Vecka med olika V-fokus

Publicerat av
Svara

En skolstart med fokus på vänskap, värdegrund, vinter och Vektor.

Vi startade terminens andra dag med en dag fylld av olika övningar med värdegrund och vänskap som tema. Vi använde idéer från boken Utmanande dialog – fördjupa dina elevers kunskap och förståelse av James Nottingham. Eleverna fick med hjälp av känslokort visa hur de känt sig vid olika dilemman kopplade till skolsituationer, samarbetslekar och diskussioner om vad en bra kompis är och hur de själva tänker för att var en bra kompis. En dag som avslutades med att en trappa för utveckling av vänskap och samarbete togs fram och nu använder vi oss av den för att elevernas egna reflektioner.

Dagarna har sedan fortsatt med ett vintertema. Hur har vi det i Sverige på vintern? Var är det vinter? Var finns snön? Hur ser träden ut på vintern? Vad gör alla djuren? Hur mår vår lilla ekorre? Vi har kombinerat faktakunskaper från filmer, digitala sidor, läroböcker och egna erfarenheter. Vi fick några timmars”snölek” under tisdagen i det skånska snöslasket, några snögubbar kom upp under rasten för att bara vid nästa rast några timmar senare ha rasat ihop av allt regn. Några elever gav sig ut på pulkaåkning, det gäller ju att passa på.

Sedan i måndags har vi varje dag tränat tillsammans på Vektor. En app som tränar matematik och minnet. Fullt koncentrerade och med en ambition om att lära sig mer kämpar eleverna. Efter bara några dagar är vi imponerade över hur målmedvetna eleverna är och hur de tar sig an de olika områdena. Att samla diamanter, samla guldmynt, brottas med djur och få medhjälpare motiverar och ger eleverna en drivkraft att fortsätta träna.

Begrepp förenar och förtydligar i matematiken.

Publicerat av
Svara

Idag skrev jag ett inlägg på Engelholms skolors bloggportal här kommer en kopia:

Begrepp behöver lyftas tidigt i lärandet av matematik och bör ha en stor plats i undervisningen av såväl yngre barn och äldre. Att kunna sätta ord på och att kunna förstå viktiga ord som vi använder i matematiska sammanhang kan grundläggas tidigt.

img_4912

ur ”Tänka, resonera och räkna i förskoleklassen”, NCM

Jämförelseorden kan man laborera med i leken, förtydliga tillsammans och upptäcka skillnader och likheter. Vi har med hjälp av screening upptäckt att det är vissa ord som barn har svårare att skilja på. Hög/låg och lång/kort förvirrar för en del men går rätt lätt att förtydliga och arbeta med. Vi valde att  jämföra pinnar och pratade om lång – längre – längst och kort – kortare – kortast. Det blev väldigt intressant när nya pinnar hämtades och plötsligt kunde en kort pinne vara lång beroende på vilken pinne man jämförde med. När undervisningen går vidare in i barnens lek då blir det ännu verkligare och de befäster kunskapen tillsammans. För att förtydliga hög – högre – högst och låg – lägre – lägst byggde vi torn av duploklossar som vi på samma sätt kunde diskutera orden med. Nu kunde vi jämföra de olika orden hög och lång, låg och kort, denna delen gav oss många roliga och lärorika funderingar och satte ord på det som var lika och olika. Det finns som tur är alltid elever som ger oss utmaningar vilket jag är väldigt tacksam för. Dessa elever ger oss frågorna som vi kan utmana undervisningen och kunskaperna med. tex  kom frågan:

– Men va? Vi är ju långa…. borde vi inte vara höga? undrade en elev.

Detta var början till en lång intressant diskussion med elevgruppen.

Ordet fler vet det allra flesta elever vad det betyder och kan visa på att de äger kunskapen, men motsatsen färre var det betydligt svårare med. Ta fram flera klossar eller färre. Dela upp konkret material så att en elev har färre än en annan,  är det samma sak som att den andre har fler än mig?  Diskutera, visa, pröva erfarenheter, jämför antal på flera olika sätt då möjliggör vi ett ökat lärande. Det gäller att laborera och visa på att ordet används i olika situationer i vardagen, ge eleverna representationer som gör det möjligt för dem att äga det, att börja använda ordet själva. Elever med en flerspråkig bakgrund behöver få möjlighet att laborera med ordet även på sitt andra språk. Ett nära arbete med modersmålslärare tror jag är viktigt för att stärka de viktiga orden ännu mer hos varje individ.

Även lägesorden behöver eleverna få äga och lära på ett praktiskt sätt. Dessa orden är beskrivande och förhåller sig alltid till något annat: tex mattan ligger under bordet, glaset står på bordet, till höger om bordet står stolar, bakom bordet finns ett fönster mm.
img_3275 img_3466 img_3463 img_3268

Kombinera lärandet genom att använda jämförelseord och lägeord i undervisningens alla olika delar och samtidigt i vardagen. Det kan vara när teckningar eller bilder sak göras, i en lek, i legobyggandet, i hemvrån, i kapprummet, på idrotten eller i samtalet vid lunchen. Diskutera likheter och olikheter, lyft de speciella egenskaper som skiljer eller ger just likheten. Pröva med olika material tillsammans för att upptäcka. Lär eleverna att upptäcka och se detaljer. Låt eleverna söka, sortera och se former och kombinera mönster tillsammans. Att kunna se och göra mönster är grundläggande i matematiken en grundsten att bygga vidare på. Samtidigt behöver eleverna träna på att sortera och se likheter och skillnader, gärna på detaljer där vissa kan ge en likhet och andra en skillnad. Detta kommer att göra eleverna uppmärksamma och hjälpa dem i lärandeprocesser oavsett ämne. Experimentera och laborera tillsammans i skapandet ger också en gemenskap och trygghet.

Hur förklarar man ett begrepp? Hur visar man vad just ett begrepp är? Detta är mitt försök till förklaring. Begrepp är innehållet i ”ordet” eller termen det som betecknar betydelsen och som ger en förklaring när vi använder termen konkret eller abstrakt. Begrepp behövs för att vi ska förstå och för att vi ska kunna använda våra förmågor och kunskaper tillsammans. Vissa begrepp har en ämnestillhörighet andra är mer övergripande.

antal
Favorit Matematik (Studentlitteratur) har matteord = begrepp som eleverna kan träna på i den digitala boken. Dessa är kopplade till varje kapitel och övningarna ger både en förståelse och synliggör termerna. Begreppen är återkommande och lärandet fördjupas och ökar efterhand tillsammans med kunskaperna. Dessa ord, begreppen,  får eleverna uppmärksamma på innehållet och lärandet i kapitlet som man arbetar tillsammans med. Jag har upplevt det som en styrka att man tillsammans kan arbeta med begreppen innan man egentligen sätter igång med kapitlet, eleverna får en gemensam förklaring och kan tillsammans utforska dem under lärandeprocessen.  Oavsett vilket läromedel eller om man undervisar utan så kom ihåg att lyfta begreppen högt! Förklara och sätt ord på dem! Använd dem tydligt, då blir lärandet enklare och tydligare.

Begrepp som siffra och tal är väldigt roliga att jobba med tillsammans, här har Mattelandet från UR lyft skillnaden i sina program med hjälp av roliga kommentarer som man lätt kan fortsätta arbeta med efter att ha sett programmen. Väldigt uppskattat hos eleverna, att först se på ett program och sedan själva få använda kunskaperna och det som de sett igen. UR har flera bra matematikprogram som jag hoppas att lärare använder i undervisningen. Titta in till dem och sök efter något som passar din undervisning och din elevgrupp. använd som ”Flippat” för att få förförståelse eller för att ge befästning av lärande.

 

Undervisning med hjälp av läromedel som ett verktyg!

Publicerat av
Svara

Sista tiden har sociala medier översvämmats av frågor om tips på läromedel och vi tipsar hej vilt – så även jag. Nu har jag mer och mer börjat fundera över om det går att tipsa vem som helst hur som helst. Läromedel är så olika och kräver olika saker av dig som lärare och brukare av dem. Är det så egentligen att du måste ha klarat dig utan läromedel ett tag för att kunna använda dem på ett riktigt sätt? För att kunna använda dem rätt och ge eleverna en utmanande och utvecklande möjlighet till lärande…

Jag ser läromedel som ett verktyg i min undervisning precis som konkret laborativt material, digitala hjälpmedel och eleverna själva. Det är i samspelet mellan de olika delarna som min undervisning blir till ett lärande, till en zon där vi tillsammans lär oss med hjälp av alla verktyg som vi just nu behöver.

Skärmklipp

Det är nog detta jag gillar bäst med ett läromedel som Favorit Matematik. Det finns så många olika sätt att ta del av uppgifter och innehåll. Det finns bra och lagom stöd i lärarhandledningarna, du kan själv utöka och förbereda dina elever utifrån de uppgifter som finns i böckerna och du kan hoppa över. Det finns interaktiva tavlor som eleverna själva kan laborera på om de behöver eller vill träna något extra. Samtidigt finns det öva och pröva sidor att använda om det behövs till läxor eller annat smått och gott. Det råder delade meningar om det mesta så du måste använda läromedel så de det passar dig, din undervisning och givetvis eleverna. Det finns uppgifter att träna mer på under fliken kopieringsunderlag i lärarhandledningen och du kan få uppgifter kopplade till de sidor där du och dina elever just nu befinner sig om du loggar in på den digitala lärarhandledningen.

Matteorden och dess träning i den digitala boken gillar jag! Att varje Kapitel/område har 10 begrepp/ord som tränas extra och som givetvis är noga genomtänkta beroende på innehållet är superbra. Nivån höjs efterhand samtidigt som de sätter sig tackvare den repetition som kommer automatiskt.

Vi har dessutom gjort egna halvbra matriser med lärandemål som vi har använt till eleverna vilket också gett dem ett stöd i sitt lärande. vi har plockat i en mall som vi tillsammans gjorde på Rebbelberga för att förenkla arbetet. du får gärna ta del av dem, men de förändras och vad vi använder till hösten vet jag inte just nu.

Matematikmatriser åk 1-3

Jag gillar upplägget att eleverna har allt samlat i en bok. Jag blir däremot skogstokig(nästan i alla fall) om eleverna bara gör utan att reflektera över sitt lärande. Det är totalt förbjudet att ”fylla i” då använder man tiden fel! Det är nog bland det första jag fick diskutera med eleverna och informera föräldrarna om. Bara för att vi råkade få/använda en lärobok i åk 3 så innebar det inte att allt skulle ”göras”, för det skulle vara fokus på lärande. De som haft svårast för detta är de sk ”duktiga” eleverna som alltid ska ligga steget före, tror de. Det har tagit tid, vi har diskuterat mycket om just ansvar för mitt eget lärande för att alla skulle se till att träna inte ”göra”.

Elever som har lätt för det utmanas på Prövasidorna, vilka brukar räcka långt. De som behöver träna mer kan göra det i den digitala boken, då får de repetition på exakt samma uppgifter vilket känns tryggt för en del elever eller på Övasidorna där det repeteras med nya uppgifter. Själv har jag haft elever som hemma haft möjligheten, tillsammans med fantastiskt engagerade föräldrar, att förbereda sig på lektionerna och därigenom få en trygghet och extra stöd på det sättet.

Hur som helst det är inte lätt att råda till något läromedel men vill man ha en hög kunskapsnivå så är Favorit Matematik ett bra verktyg.

För mer tips om just Favorit Matematik så titta in i Facebook-gruppen Favorit Matematik tips och idéer eller på Studentlitteraturs egen sida.

 

Första veckan med lärobok till eleverna

Publicerat av
Svara

Oj, oj, oj! Tur att man har rutin! Annars hade vi väl varit superstressade redan! Vi har inte hunnit alls så långt som vi borde enligt terminsplanen.

Det spelar ju ingen roll alls, huvudsaken är att vi har ett lärande och att eleverna mår bra i arbetet. I starten tar repetition längre tid, vi måste bli lite ”skol klara”, bli beredda för lärande, nya elever ska lära kännas och bli en del av gruppen. Detta gör vi delvis genom att tillsammans lära oss olika saker.

Så till upplägget v.1:

favortimatteNu har alla eleverna loggat in på sina digitala böcker, arbetat igenom de första 4 sidorna och haft ordentligt med tid för att se hur läromedlet fungerar. Jag gillar upplägget!  Varje del har huvudräkningsuppgifter där man benämner begrepp som kan göra det lite klurigt och utmanar alla. Dessa kan diskuteras och bli större eller bara en enkel snabb starter. Genomgångar på varje område med digital tavla/ smartboard via den digitala lärarhandledningen som verkligen är ett plus. Där finns både färdigstrukturerade genomgångar och tavlor där jag själv styr genomgången. Dessa har sedan direkt kopplade träningsuppgifter där eleverna kan träna i sin egen takt. Det finns öva-uppgifter som ger mer träning eller pröva-uppgifter som ger utmaning för eleverna. Även kopieringsunderlagen är direkt kopplade till de områden vi arbetar med men man kan också söka efter begrepp som man känner att eleverna eller någon elev behöver träna mer på. Dessutom finns det till varje kapitel matteord där man tydliggör begreppen som just nu bearbetas. dessa når eleverna via sina digitala böcker och där finns även övningsuppgifter till begreppen.

Självklart gäller det att anpassa allt man arbetar med till eleverna och deras kunskaper. Jag är rätt säker på att vi inte kommer att hinna arbeta med allt i boken för vi är inte riktigt vana, men den kommer att vara ett stöd. Vi väljer att vid ett tillfälle i veckan arbeta med problemlösning. Då styr vi in eleverna i grupper och de tänker utifrån konceptet i Eldorado & fyrfältsblad från NCM som vi haft sedan åk 1. Problemlösningsuppgifterna var bra och kluriga men lite fel i formuleringen tycker nog vi men det fixade vi till 🙂 . Helheten är bra och ger mig som lärare möjlighet att fokusera på lärandet. Vi kopplar dessutom matriser till  varje kapitel så eleverna ser sitt lärande. Det blir tydligt tänker vi.

Man ser både elev sidorna och allt extra material i lärarhandledningen och ännu mer finns alltså digitalt. Så här ser lärarhandledningen ut:
uppslag 2 uppslag 1

 

 

 

Övertalad, nästan övertygad!

Publicerat av
2

Min vision om hur en skola fungerar ligger till grund för att jag nu tagit ett steg jag inte trodde på för bara några dagar sedan.
Först lite av mina tankar…

Eleverna ska inte vara beroende av vilket arbetslag eller vilka lärare de går hos. Vi måste kunna säga: Så här arbetar vi! En trygghet i skolans vision och den värdegrund vi tillsammans sätter så väl i undervisningen som i bemötande.

Det skär i mig när jag hör föräldrar fundera och prata om var/hos vem/vilka deras små barn kommer att hamna. Jag vill arbeta på en skola där vi tillsammans står på samma grund, ger eleverna samma upplevelser och ser på lärande på samma sätt. För mig är det värdefullt att vi ser eleverna som allas elever – skolans elever!

Så till fakta och summering av ett läsårs arbete med matematikgruppen:

Visionen och syftet var att skapa en gemensam bedömningsgrund, se över läromedel och screeningmaterial så att vi fick en helhet och enighet på skolan. Ett arbete som vi startade med öppna sinne men också en del funderingar. Det kändes stort, på gränsen till övermäktigt men ändå hade vi en vision om att lyckas. Under första tillfället satte vi oss in i skolverkets bedömningsmaterial och via RUC (Regionalt utvecklingscenter) i Halmstad fick vi en föreläsning där önskan var just information om materialet. Vi avvaktade och åkte i slutet av januari på en föreläsning med stora förväntningar. Tyvärr blev det platt fall, vi var minst lika förvirrade vad det gällde materialet men också i en ny fas, vi var själva tvungna att ta oss vidare. Förmågorna lyftes, vi arbetade i dokument via GAFE tillsammans och vi var kreativa dagen efter föreläsningen. Ingen av oss var helnöjd, resultatet var otydligt för de yngre eleverna och även på mellanstadienivå var vi osäkra på just tydligheten mot eleverna. 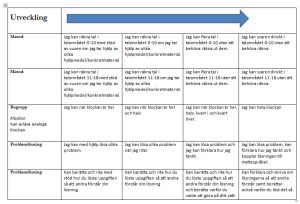Vad vi skulle bedöma är inget konstigt men ht 2014 åk2 nr 1just HURet och hur vi gör det synligt för eleverna brottades vi med. Någon dag passerade och vi blickade mot nya matriser, bl a matriser som vi i mitt eget arbetslag redan använt (som ni ser delar av i bloggen). Kunde vi via dessa tänka om, få en likhet i tänket som våra kollegor i svenskgruppen lagt upp? Jag och Sarah (en kollega i matematikgruppen som jobbar med de yngre barnen) satte oss och började formulera om och till, sakta byggde vi upp en fungerande matris som vi skulle kunna få att fungera genom att den i starten fick vara et arbetsmaterial som anpassas efterhand.

Nästa träff i gruppen skulle handla om läromedel och screeningmaterial. En kollega hade beställt allt som fanns på SLI.se för att vi skulle kunna titta ordentligt, jämföra innehåll, svårighetsgrad mm. Vi hade  samlat ihop allt material som vi hittade på lågstadiet över olika läromedel. Sedan tidigare har vi på Rebbelberga skola full uppsättning lärarhandledningar och läroböcker i Eldorado från Natur&Kultur från åk F till åk 6. Vi är väldigt nöjda med nivån på undervisningen och lärandet som detta läromedel håller, men ser också svårigheter för våra sva-elever eftersom läromedlet kräver hög läsförståelse och ordförståelse. Under en stund bläddrade vi fram och tillbaka i de olika böcker täckte i stort sett hela konferensbordet, men vi insåg rätt fort att vi alla hela tiden kom tillbaka till ett och samma läromedel. Vi hade fokus talförståelse för det är oftast den delen eleverna behöver struktur och färdighetsträning i, övriga delar i matematiken känner vi oss säkra på att vi ändå får in i undervisningen och på en rätt hög nivå bl a genom att alla lärare fått kollegial fortbildning via matematiklyftet.
eldorado 2 eldorado 5 favoritmatematik 2 favoritmatematik 4 Nu var det Favorit matematik från Studentlitteratur som vi alla landade tillbaka i, ett läromedel som kändes komplett i talförståelse men vi saknade några andra delar. Vi har flera av oss varit i kontakt med deras försäljare, Peter Falkheden, i andra sammanhang så vi tog snabbt kontakt med honom och fick ett möte inbokat, bara några dagar efter, där vi skulle få materialet presenterat för oss. En måndag för 2 veckor sedan kom Peter och hade en presentation om hela materialet. (Han var lika medveten som mina kollegor om min inställning till läromedel i de lägre åldrarna.) Plötsligt öppnades ett läromedel som via digitala möjligheter svarade på alla våra frågor,många kritiska sådana, delarna som vi saknat fanns såklart med. Själv hade jag under ett läsår suttit på lärarhandledningar i åk 2 som var en större guldgruva än jag under året anat, för jag hade ju varit fullt nöjd med det vi hittade i kopieringsunderlag mm. Vi fick en visning av ett läromedel som hade allt, färdiga ”tavlor” vid lektioners uppstart – man behövde inte längre lägga tid på att hitta rätt smartboard produkter, huvudräkningsuppgifter kontinuerligt, problemlösning, kontinuerligt finns summativa tester = screening möjligheter, varje uppslag har via lärarhandledningen kopplat extra träning via kopieringsunderlag, mm. Det kändes som om listan blev längre och längre över de saker vi önskade och möjligheterna otroliga. Dessutom kändes materialet tydligt för de elever som ännu är nya i svenska språket.

Här satt jag alltså med kollegor och en försäljare, Peter Falkheden, och var plötsligt överväldigad över ett läromedels möjligheter. Jag som är skeptisk till läromedel började känna att –  ja, men det kanske ändå kunde vara skönt. Senast dagarna innan hade jag ifrågasatt i socialamedier varför man i åk 1-3 behövde läromedel i matematik….Ajdå! Men man måste Våga! Våga ändra på sig, våga testa något nytt! Våga förändra sina åsikter!

Det som övertygade mig var framför allt Favorit matematiks möjligheter, som är en bråkdel om man inte satt sig in i allt som finns digitalt. Dessutom önskade vi en likhet på skolan. En likhet som gav eleverna samma grund och möjligheter. Screeningmaterial hade vi i form av ”Förstå och använda tal” men vi saknade en helhet och mer kontinuerlig screening. Allt fanns nu i materialet så vi hittade en helhet. I processen fanns speciallärare, lärare från både 4-6 och 1-3 så alla typer av lärare var representerade, dessutom arbetar jag själv till viss del som matematikutvecklare i kommunen. Vi presenterade våra tankar för vår rektor, Stig Hasselgård, och efter snabb dragning på konferens där lärarna i de olika arbetslagen fått säga sitt via ett GAFEdokument och en kortare överläggning så var satsningen ett faktum. Vi kommer att gå in och under ett läsår arbeta efter Favoritmatematik i åk 1-5. Åk 1 kommer att använda lärarhandeldningarna men inte elevböckerna övriga kommer att ha Favoritmatematiks Mera-bok för respektive årskurs. Det kommer bli ett år som ska utvärderas efter konstens alla regler för målet och visionen är högre måluppfyllelse och alla elever ska nå  målen. Vi tänker oss nog att vi successivt kommer att följa upp och prata om hur vi upplever läromedlet och dess funktioner.

Jag kommer att försöka blogga kontinuerligt om hur det går här på min blogg, reflektera ärligt över hur det känns, hur det går och hur allt fungerar.

IMG_2227Förskoleklassen kommer att till största delen arbeta efter ”Tänka, räkna och resonera” av Görel Sterner bla från NCM. åk 6 fortsätter med Eldorado vilket de eleverna är vana vid sedan åk 1 både utan och med lärobok.

 

Geometri & matematiklyft tillsammans med algoritmträning!

Publicerat av
Svara

Blir inte alls lika mycket uppdateringar här som tänt men det ska jag försöka bli bättre på.

IMG_4062Just nu är våra elever och vi lärare mitt uppe i ett arbete med geometrifokus blandat med inlärning av ren algoritmräkning i addition och subtraktion. Kombinationen är bra, praktiskt arbete blandas med träning på räknestrategi.

begreppsord geometri

 

Fokuset i geometrin har varit att muntligt diskutera och kommunicera om former och figurer – inga frågor är onödiga för de hjälper oss i lärandet. Undervisningen sker ofta i 3-4 grupper(54 elever). Sedan har vi fotograferat former och figurer på skolgården som nu är bildstöd i varje elevs powerpoint. Här visar de sina kunskaper om former och figurer. Tillsammans har vi skapat ett dokument med begreppsord och namn på former och figurer som eleverna tyckte behövdes. Det har varit ett lärande på elevernas grund de har själva kommit fram till vad de behöver lära för att kunna beskriva formerna och det är viktigt att det är rätt matteord(annars kan man få utslag 😉 ). Vi lärare har tillsammans i modulen geometri i matematiklyftet fått utmaning för våra tankar och det har utvecklat oss ännu mer. Vi har använt ord och begrepp som vi aldrig gjort innan och vi har också nått betydligt högre nivåer i begreppskunskap.

Elevernas fokus har verkligen varit på lärandet och vi är fortfarande inte klara, nu ska vi utforska de tredimmesionella figurerna. Eleverna ska få veckla ut dem, tillverka egna och fundera på de olika formerna som de sedan består av.
IMG_4052 IMG_4059 IMG_4055

Parallellt har vi en period av träning på att lära sig räkna ut 2-siffriga tal med hjälp av algoritmer i addition och subtraktion. det har varit enbart fokus på strategin inte så mycket på varför man gör som man gör men det har ändå blivit en diskussion om vad de olika siffrorna i talen betyder, helt på elevernas egna initiativ och det har verkligen blivit ett lärande. Eleverna har fått sitta i grupper och tillsammans träna och testa, de har tränat sig på att kommunicera och argumentera.

 

Matematiktankar!

Publicerat av
2

Att läsa olika inlägg på sociala medier, forskar rapporter, blogginlägg och  olika sorters pedagogisk litteratur sätter igång mina tankar. Dessa försöker jag automatiskt att koppla  till mina egna erfarenheter som lärare, 23 år i bagaget. Jag kommer aldrig att vara färdig med mitt lärande och min undervisning kan utvecklas så länge jag arbetar som lärare. Mitt mål är att få så många elever så långt i sitt lärande som det är möjligt. Provocerande kommentarer utvecklar mest för då måste jag verkligen fundera över hur jag tänker och varför jag gör som jag gör.

Jag har tillsammans med mina kollegor haft lärarhandledningar i ryggen och läroplanen är vi väl insatta i. Det är ofta en trygghet att ha något som man kan luta sig mot. Jag vet vilka områden vi kommer att behandla och jag vet vart jag vill att eleverna ska nå. Min uppgift är att lägga upp lektionerna så att både jag och eleverna får koll på var vi befinner oss i utgångsläget och att vi gemensamt kan se nästa nivå. Detta är inte alltid enkelt och det kräver flera olika steg och lektioner vissa gånger nästa gång kan det ta 10 minuter. Jag vill utmana eleverna, få diskussioner om talen, begreppen, strategier, metoder och kunna reflektera och analysera matematikinnehållet. Min uppgift som lärare är att vara vägen mellan det muntliga, bilderna och matematikspråket. Att få hjälpa eleverna att översätta till matematikspråket är en häftig resa att få vara med på.

Elevlösningar från åk1 på Toftaskolan i Ängelholm.

Elevlösningar från åk 1 på Toftaskolan i Ängelholm.

Mina bästa lärande situationer är inte när jag har planerat i timmar hur lektionerna ska utformas utan oftast de där lektionerna som jag funderar på utifrån att fått någon ide. Just nu är det matematiklyftet som ger mig flest ideer. När jag sitter tillsammans med alla de lärare som jag handleder får jag så många nya utvecklingsmöjligheter av mina lektioner. Ibland kanske jag i dessa lägen utmanar mer än någonsin, förhoppningsvis sporrar jag lärarna i grupperna lika mycket som jag själv sporras. Matematiklyftet är fantastiskt uppbyggt med dessa lektioner som ska genomföras utifrån de didaktiska eller strukturella  tankar som modulen bygger på. Eftersom jag handleder i 2 moduler så genomför jag uppgifter från olika delar så som det passar in. Jag tycker om att vi genomför problemlösning som utamanar elevernas tankar längre än vad vi hade gjort om vi bara sett till innehåller i läroböckerna. Jag vill inte se begränsningar alla elever ska utmanas och få resonera på sin nivå. Barn på förskolorna pratar delar tidigt i vardagliga situationer, när de kommer till skolan så ska vi leda dem in på nästa nivå. Vi lärare måste översätta och ge dem möjligheter att överföra sin kunskap till nya konkreta material. Vi utgår ifrån att begreppen vi använder inom bråk har eleverna hört länge –  vi ska här översätta dessa till matematikspråket och få eleverna att se den naturliga kopplingen mellan ordet och siffrorna och symbolerna. Ovan ser ni resultat av ett arbete med fjärdedelar och olika möjliga lösningar med kvadrater med 4*4 rutor. Eleverna fick både bygga med multilink-klossar och sedan översätt till samma former på papper.

När jag är på tå i mina tankar och undervisning kan jag inte alltid skriva ner min struktur på hur jag kommer att undervisa den växer fram i dialogen med eleverna. Detta är väldigt tydligt på tisdagar, då har jag nämligen samma lektion 3 ggr. Lärandemålen är detsamma men de blir aldrig identiska, det är så mycket intressantare och jag blir mer engagerad över att undervisa såhär. I starten av ett nytt område eller i slutet när något ska knytas ihop så utmanar jag gärna för att tydliggöra deras lärande både för mig själv och för dem. Jag har inte denna sortens undervisning hela tiden för vissa lektioner är träningslektioner då eleverna i lugn och ro får träna på det vi den sista tiden diskuterat och resonerat om.

 

Förstå och använda tal – en skatt för diagnos och analys

Publicerat av
3

Förstå och använda talNär samarbete sker i utvecklingssyfte mellan kompetenser av olika slag sker ibland små underverk.

Att få förståelse för varför resultat ska samlas in, att få lärarna uppmärksamma på ”Förstå och använda tal-diagnosernas” syfte och verkan i den egna undervisningen har varit ett uppdrag jag haft under några år både lokalt på den egna skolan och även centralt i kommunen. Det har i omgångar irriterat mig att processen tar så lång tid och återkopplingen med tydliga diagram har inte kunnat levereras tillbaka till lärarna omgående. För att jag som lärare ska kunna se nyttan med ett analysredskap i min undervisning så behöver jag få tillbaka diagram direkt i anslutning till att jag registrerar mina elevers resultat. Då kan jag ta det till min undervisning och omedelbart omsätta det i praktiken.

När man bestämmer sig för att ta hjälp av den kompetens vi har i kommunen på RiKT(=resurs för IKT) och får gehör för tankar och sedan hjälp som visar  på förbättringar som blir så rätt, då blir det glädje och lycka. Att äntligen vara nära att nå mål och vision för ett långt arbete känns så skönt, när man diskuterar och pratar samma språk som ger ett tydligt resultat.

Vad kan bli bättre än att läraren vid inmatning av sina elevers resultat får ett tydligt stapeldiagram för dels hela gruppen, flickor och pojkar för sig och dessutom ett spindeldiagram som påvisar hur stor procent av eleverna som lyckat på varje enskild uppgift?

spindeldigramNu har vi nått fram så detta sker , varje skola kommer att få sin egen mall, de får analysredskap som de direkt kan använda sig av. Vill man se resultaten från sina diagnoser även på vårterminen så är det bara att använda mallen och få fram lika snygga diagram.

Utveckling sker när vi samarbetar över gränserna på alla håll både inom skolor och mellan skolor. Lägger vi in resultaten så de blir synliga för alla kan vi ta lärdom av varandra, hjälpas åt att höja resultaten och följa eleverna i både högre och lägre årskurser.

När vi som arbetar med utveckling av olika slag samarbetar sker även utveckling av den delen. Vi hittar vägar där vi kan hjälpas åt där de olika utvecklingsområdena sammanflätas och ger större och bredare möjligheter genom analyser att öka kompetenserna i verksamheterna.

Det som nu blev resultatet hos oss gör att vi kan tänka i vidare perspektiv och se till att utveckla nya hjälpmedel för lärarnas analysarbete av den egna undervisningen. Ett analysarbete som är viktigt för elevernas individuella kunskapsutveckling i slutänden. När lärare börjar se resultat och utifrån dessa förändrar och utvecklar sin undervisning då får vi chansen att se ett ökat lärande hos eleverna. Kan vi som lärare vara öppna och diskutera våra resultat och samarbeta så blir det ett kollegialt lärande med än större effekter.

Tilläggas till detta ska göras att resultaten samlas in avidentifierade och endast pojke/flicka är skrivet. Varje lärare kan själv däremot ha med namn på sina elever så länge de vill och utifrån detta hantera även individuella skillnader.

Tack till Stig Hasselgård som såg möjligheterna och vinsterna med detta och som nu gjort våra snygga mallar och dessutom fixat till årets resultat väldigt kvickt!